Definition and Types of Algebraic Expressions
p.1. Mathematical Symbols and Expressions
In the mathematical language, we use special «letters», called mathematical symbols; пwhen combined, they form special "words" called mathematical expressions.
0,1,2…9
Greek α,β,…,ω,Λ,Σ,Ω
English GCD,LCM,$ V_{pyr} , S_{cr} $
Other operators: $2^3, {\sqrt x}, \Rightarrow, \&, {\circ}, {\int}, {\sum}$
Other signs: $\forall, \exists, \to, \bot$
The list of mathematical symbols is constantly updated. No wonder, since everyone is free to invent a hieroglyph-symbol of their own, explain its meaning via definition and propose the rules of its application. If the symbol turns out to be handy and functional, then, over time, it will appear in other works and begin its independent journey around the world.
Suppose, according to the rules, we build mathematical expressions that consist of various numbers (i.e. digits, fraction bars, and decimal points), arithmetic operators, rational powers, roots and brackets:
For example, $(1+5^2):3\frac 14 , \frac {4+3,5}{(12-6^3)+5} , \frac 12 - \frac 13 \cdot (-\sqrt 9) $
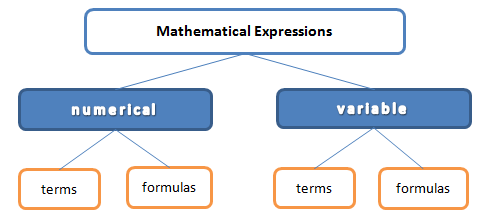
Expressions of this type are called numerical terms.
Let us add comparison signs to the list of the allowed mathematical symbols: $(1+5^2):3\frac 14 \gt 7, \frac {4+3,5}{(12-6^3)+5} \lt 0, \frac 12 - \frac 13 \cdot (-\sqrt 9) = 1\frac 12$
Expressions of this type are called numerical formulas.
When compared to a term, a formula has an additional feature: it can be "true" or "false". The three formulas given above are true. But 2+2=5 is a false numerical formula.
p.2. Variable Definition and Meaning
In practice, when carrying out calculations, we often find repeated patterns where only one value changes, while others remain constant. For example, we want to calculate the area of slabs with the length of 7, 10, and 15 m, and the same width of 4 m. Then, S_1=4∙7=28 m^2,S_2=4∙10=40 m^2,S_3=4∙15=60 m^2. These calculations can be generalized as follows: S=4a, where the first factor is the constant width of 4 m, and the second factor is the variable length of a m. This generalization is called "introducing a variable"; it is convenient, since it simplifies our calculations.
By the type, mathematical expressions with variables can also be terms or formulas.
Variable terms: $(1+a^2):3 \frac 14 - b, \frac {4+mn}{(12-k^3)+5}, \frac 12 - \frac {1}{b^2+1} \cdot (-\sqrt 9) $
Variable formulas: $(1+a^2):3 \frac 14 - b > b, \frac {4+mn}{(12-k^3)+5} < 0, \frac 12 - \frac {1}{b^2+1} \cdot (-\sqrt 9) = f-3 $
p.3. Algebraic and Transcendental Expressions
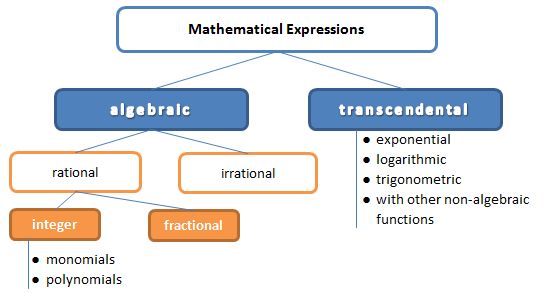
Depending on the set of allowed operations, mathematical expressions are divided into algebraic and non-algebraic (transcendental).
ЕIf an algebraic expression does not contain division by a variable or extracting a root of a variable (or raising a variable to a fractional power), then it is called an integer expression.
Examples of integer expressions:
$7, \frac {3a^2}{5}+48, (\sqrt 7b-4c^3)^5$ - terms $b-\frac 32 = 8,28c^2 > \sqrt 2$ - formulas
If an algebraic expression, in addition to the features of an integer expression, contains division by a variable, then it is called a fractional expression.
Examples of fractional expressions:
$\frac 7m, 3a^2 + \frac {48}{k-4}, (\sqrt 7b-\frac {4}{c^3})^5$ - terms $b-\frac {2}{2+a} = 8,28c^2 > \frac {\sqrt 2}{5k}$ - formulas
Integer and fractional expressions are combined into the class of rational expressions.
If an algebraic expression contains extracting a root of a variable (or raising a variable to a fractional power), then it is called an irrational expression.
Examples of irrational expressions:
$\sqrt a - \sqrt[3]{b^4}, 1 + a^{\frac 23}, \frac {1 - \sqrt a}{1 + \sqrt b}$ - terms $\sqrt[3]{a} = 34, 22 - \frac {8}{1=\sqrt b} \le 1+k $ - formulas
p.4. Examples of Problem Solving
Example 1.Write down the numerical formula and check if it is true: twice the product of the numbers 75 and $3 \frac 13$ is half of the difference between the numbers 1440 and 480.
Solution:
The numeric formula: $2 \cdot 72 \cdot 3 \frac 13 = \frac{1440-480}{2}$
The value of the expressions on the left $2\cdot72\cdot3 \frac 13 = 2\cdot24\cdot3\cdot \frac{10}{3}=480$
The value of the expressions on the right $\frac {1440-480}{2} = \frac {960}{2} = 480$
The values of the expressions on the left and on the right are equal, the formula is true.
Answer: the formula is true
Example 2. Given $a = 3\frac 14$ and b=3.5, evaluate the algebraic expression 2

